Фракталы

Множество Мандельброта — классический образец фрактала
Морозные узоры на окне, замысловатая и неповторимая форма снежинок, сверкающие молнии в ночном небе завораживают и пленяют своей необыкновенной красотой. Однако мало кто знает, что все это является сложными фрактальными структурами.
Бесконечно самоподобные фигуры, каждый фрагмент которых повторяется при уменьшении масштаба, называются фракталами. Сосудистая система человека, система альвеол животного, извилины морских берегов, облака в небе, контуры деревьев, антенны на крышах домов, клеточная мембрана и звездные галактики — все это удивительное порождение хаотического движения мира есть фракталы.

Фрактальная форма подвида цветной капусты (Brassica cauliflora)
Первые образцы самоподобных множеств с необычными свойствами появились в XIX веке. Термин «фракталы», который происходит от латинского слова «fractus» — дробный, ломанный, был введен Бенуа Мандельбротом в 1975 году. Таким образом, фрактал представляет собой структуру, состоящую из частей, подобных целому. Именно свойство самоподобия резко отличает фракталы от объектов классической геометрии.
Одновременно с выходом в свет книги «Фрактальная геометрия природы» (1977 год) фракталы получили всемирную известность и популярность.
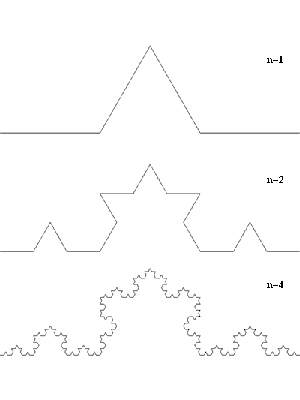
Кривая Коха
Важно отметить, что термин «фрактал» не является математическим понятием и в связи с этим не имеет строгого общепринятого математического определения. Более того, термин фрактал употребляется относительно любых фигур, обладающих какими-либо из нижеперечисленных свойств:
- Нетривиальная структура на всех шкалах. Это свойство отличает фракталы таких регулярных фигур, как окружность, эллипс, график гладкой функции и т.п. Немаловажным является тот факт, что увеличении масштаба фрактала не приводит к упрощению его структуры, то есть на всех шкалах мы видим одинаково сложную картину, в то время, как при рассмотрении регулярной фигуры в крупном масштабе, она становится подобна фрагменту прямой.
- Самоподобие или приближенное самоподобие.
- Метрическая или дробная метрическая размеренность, значительно превосходящая топологическую
- Построение возможно лишь с помощью рекурсивной процедуры, то есть определение объекта или действия через себя.
Таким образом, фракталы можно разделить на регулярные и нерегулярные. Первые являются математической абстракции, то есть плодом воображения. К примеру, снежинка Коха или треугольник Серпинского. Вторая разновидность фракталов является результатом природных сил или деятельности человека.

Фрактальное дерево
С каждым днем фракталы находят все большее и большее применение в науке и технике. Главной причиной столь активного интереса к фрактальным структурам является тот факт, что они как нельзя лучше описывают реальный мир. Приводить примеры фрактальных объектов можно бесконечно долго, они повсюду окружают нас. Фрактал как природный объект представляет собой яркий пример вечного непрерывного движения, становления и развития.
Фракталы нашли широкое применение в компьютерной графии для построения изображения природных объектов, например, деревьев, кустов, горных массивов, поверхностей морей и прочее. Эффективным и успешным стало использование фракталов в децентрализованных сетях. К примеру, система назначения IP-адресов в сети Netsukuku использует принцип фрактального сжатия информации для компактного сохранения информации об узлах сети. Благодаря чему, каждый узел сети Netsukuku хранит всего 4 Кб информации о состоянии соседних узлов, более того любой новый узел подключается к общей сети без необходимости в центральном регулировании раздачи IP-адресов, что, например, активно применяется в сети Интернет. Таким образом, принцип фрактального сжатия информации обеспечивает максимально устойчивую работу всей сети.
Весьма перспективным является использование фрактальной геометрии при проектировании «фрактальных антенн».
В настоящее время фракталы стали активно использоваться в нанотехнологиях.
Особенно популярны фракталы стали у трейдеров. С их помощью экономисты производят анализ курса фондовых бирж, вальных и торговых рынков.
В нефтехимии фракталы применяются для создания пористых материалов. В биологии фракталы используются для моделирования развития популяций, а также для описания систем внтренних органов.
Даже в литературе фракталы нашли свою нишу. Среди художественных произведений были найдены произведения с текстуальной, структурной и семантической фрактальной природой.
