Мы все ежедневно работаем с вероятностями, или, другими словами, с шансами и рисками, даже когда этого не осознаем.

Например, когда вы покупаете лотерейный билет или просто переходите дорогу — вы имеете дело с вероятностью.

Против ставок?

Вероятность — это суть азартных игр. Действительно, именно азартные игры подтолкнули к первой работе с вероятностью, математическим лицом шанса или риска. Владельцы казино или букмекеры должны достаточно хорошо представлять себе вероятность, чтобы большую часть времени оставаться в выигрыше, в противном случае они бы не получали прибыль. Но им приходится подавать шансы под таким соусом, чтобы они казались людям привлекательными. Есть несколько способов.

На скачках букмекеры показывают шансы лошадей, выражая их отношением, как здесь:

Жуткий вестник 20:1

Неженка 4:1

Странный кварк 8:1

Тангенс 7:1

Честная Бэт 5:1

Легко понять, в чем соль, если представить их в виде дробей. Шансы 20:1 означают, что букмекер думает, что Жуткий вестник имеет 1 шанс из 20 на победу, или 1/20. Шансы Неженки значительно больше — 1/4. Если мы сложим шансы на всех лошадей в виде дробей, сумма должна быть, согласно математическим законам, равна 1. Так, конечно, никогда не происходит, потому что букмекеры извлекают прибыль из разницы между общей суммой ставок и общей суммой выплат. На данных скачках, сумма равна:

1/20 + 1/4 + 1/8 + 1/7 +1/5

0,05 + 0,25 + 0,125 + 0,142858 + 0,2

= 0,767857

Разница между результатом и единицей — 0,232143, это значит, что букмекер извлекает чуть более 23% прибыли (при условии, что ставки были распределены равномерно).

Очевидно, что букмекерские шансы не имеют отношения к реальным шансам, — букмекеры преуменьшают шанс каждой лошади на победу.

Реальная вероятность должна давать в сумме 1, так как обязательно будет одна лошадь-победитель (если только все лошади не упадут или не будут дисквалифицированы).

Лотерея

Другие виды азартных игр предлагают маленький шанс на действительно большой приз, но довольно большой шанс на маленький выигрыш. Многие государственные лотереи действуют таким образом. Шанс выиграть джек-пот очень малы, обычно 1 на много миллионов, но есть значительно больший шанс (возможно, даже 1 к 25) выиграть очень маленький приз, например £10. Это уловка, она успокаивает людей, которые осознают, что шанс выиграть джекпот — крошечные, но у них, по меньшей мере, высокий шанс не потерять все вложенные деньги. В рекламе может говориться о «50 000 призов еженедельно» или чем-то в этом роде. Как мы видели в главе 9, упоминание большого числа призов привлекает; знаменатель игнорируется, т. е. мы не думаем о шансе как 50 000 на (допустим) 3,5 миллиона, или попросту 1 к 70.

Игровые автоматы действуют по тому же принципу ступенчатых платежей, предлагая разумный шанс на маленький выигрыш, но маленькую вероятность на большой куш. Небольшой выигрыш вдохновляет игрока попробовать снова, что может закончиться потерей большой суммы.

Снова и снова

Иногда бывает полезно знать вероятность более чем одного события.

Возможно, мы хотим знать:

• вероятность, что случится А или В
• вероятность, что случится и А, и В

Чтобы выяснить альтернативные шансы (А или В), мы складываем вероятности. Чтобы выяснить кумулятивные шансы (А и В), мы умножаем вероятности.

Предположим, вы подали заявление на две вакантные должности. На первую должность претендуют пять одинаково квалифицированных соискателей (включая вас), т. е. шанс получить работу 1 к 5, или 0,2. На вторую должность претендуют только 4 квалифицированных соискателя, т. е. ваш шанс — 1 к 4, или вероятность 0,25.

Шанс на то, что вам предложат одну или обе работы:

0,2 + 0,25 = 0,45 (45%)

Шанс, что вы получите обе работы:

0,2 х 0,25 = 0,05 (или 5%)

В восемь раз вероятнее, что вам предложат одну работу, а не две.

Шанс, что вам предложат одну работу, но не две — это разница между шансом на одну или две и шансом на предложение двух работ:

0,45 – 0,05 = 0,4 (40%)

Наиболее вероятный исход, таким образом, что вы не получите ни одну (простите), а следующий по вероятности — что вам предложат только одну.

Больше одного пути

Обычно самый простой способ увидеть принципы, по которым вычисляются вероятности, — представить себе бросание монеток и игральных костей.

Монета более однозначна: она может упасть либо орлом, либо решкой. Если это честная монета и равновероятно может упасть на одну из сторон, шанс получить орла — 1/2 (0,5 или 50%), и шанс получить решку также равен 1/2 (0,5 или 50%). Если мы бросим монету дважды, мы снова можем получить орла или решку. Вероятность для двух бросков:

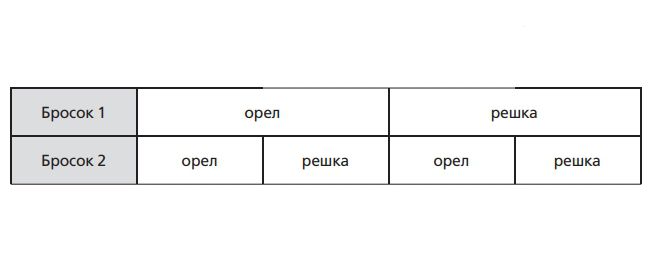
Теперь возможно 4 результата: орел, затем орел; орел, затем решка; решка, затем орел; решка, затем решка. Для многих целей «орел затем решка» — это то же самое, как «решка, затем орел». Шанс двойного орла — 1/4; шанс двойной решки — 1/4; шанс на один орел и одну решку — 1/2.

Количество вероятных итогов возрастает, если мы бросаем монету больше раз, а шанс на получение при каждом броске орла или при каждом броске решки, неважно чего, — сокращается.

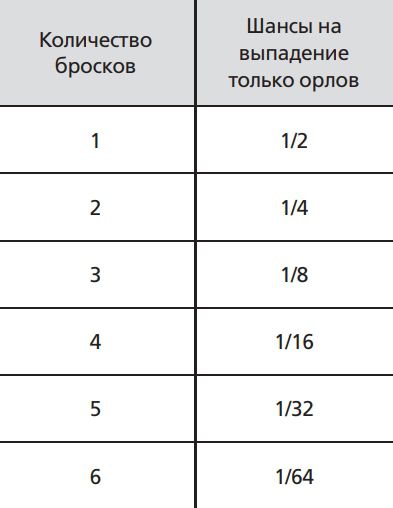
Шанс на орла при каждом броске равен 1/2ⁿ для броска под номером n. Шанс на решку при каждом броске также равен 1/2ⁿ.

Шанс на выпадение либо всех орлов, либо всех решек равен 2 х 1/2ⁿ или 1/2^n–1:

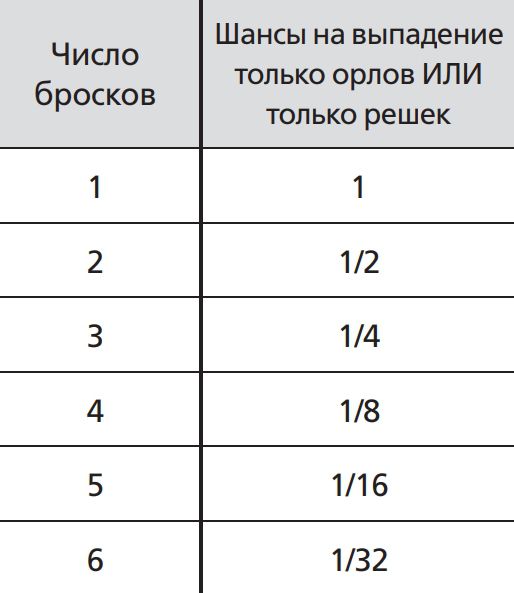
1 к 6

С игральными костями проблема становится более сложной, так как возможных итогов для каждого броска кубика — шесть. Используются те же расчеты, но теперь в степень возводится 6, а не 2. Шансы получить пятерку (или любое другое число) при каждом броске — в таблице справа.

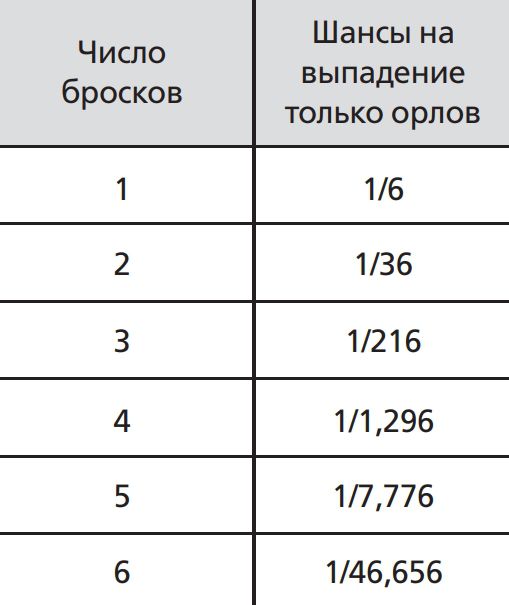
Если вы бросаете два кубика, шанс получить любой дубль равен 6^n–1.

Поскольку вы бросаете не один раз, вероятность для различных комбинаций становится более сложной. Когда нас интересует сумма очков, комбинации могут быть разными для одной суммы (см. таблицу внизу).

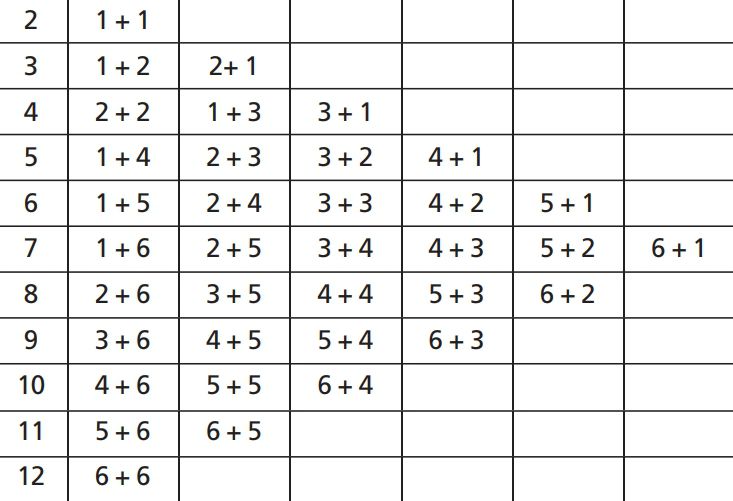
Наиболее вероятное число с двумя игральными костями — 7, так как имеется шесть способов получить 7. Это означает, что вероятность выбросить 7 равна 6/36 или 1/6. Если у вас есть выбор при игре в кости, ориентируйтесь на семерку.

Если в комнате находится 30 человек, велика вероятность, что по крайней мере у двоих из них совпадут дни рождения.

В эту часто транслируемую статистику трудно поверить. Кажется, что это противоречит здравому смыслу.

Есть два способа работы с вероятностью. Методы первого мы рассматривали в 20-й главе. Он называется частотная вероятность. Другой метод — байесовский, разработанный английским математиком Томасом Байесом (1702–1761), и он гораздо сложнее.

В году 365 дней (если он не високосный). Следовательно, существует 1/365 шансов, что ваш день рождения выпадет на определенный день. Если сравнивать себя с всего одним человеком, тогда шанс, что ваш день рождения совпадет с его днем рождения, будет 1/365

= 0,0027

Но не забывайте, что интерес вызывает не только ваш день рождения. В комнате 30 человек, что дает на 30 х 29 возможных пар дней рождения, или 870. Теперь вы, наверное, понимаете, почему так вероятно, что будет один двойной день рождения.

Поменяем задачу

Вместо того чтобы думать о шансах двойных дней рождений, подумайте о шансах людей, чьи дни рождения не совпадают, у которых нет пары в комнате с 30 людьми.

Когда есть только два человека, шанс, что их дни рождения не одновременны, равен

1 — 1/365 = 364/365 = 0,997

Если добавим третьего человека, у нас будет три использованных дня рождения, следовательно, только 363 неиспользованных дня. Теперь шанс, что их дни рождения не совпадут, равен

364/365 х 363/365 = 0,992

Добавьте еще одного человека, и шанс будет

364/365 х 363/365 х 362/365 = 0,984

Продолжим. К тому моменту, когда у вас будет 30 человек в комнате, шанс, что ни одна пара дней рождений не совпадет, равен 0,294 — почти 30%. Это означает, что есть вероятность 70%, что, по крайней мере, два человека родились в одни и тот же день. Момент, когда вероятность приближалась к 50%, прошел, когда в комнате было 23 человека. К моменту, когда в комнате будет 57 человек, шанс на парный день рождения — 99%.

Еще одно изменение

Байесовский подход к вероятности сильно отличается. Он может работать от одного набора вероятностей, чтобы вывести другую, связанную с ними вероятность.

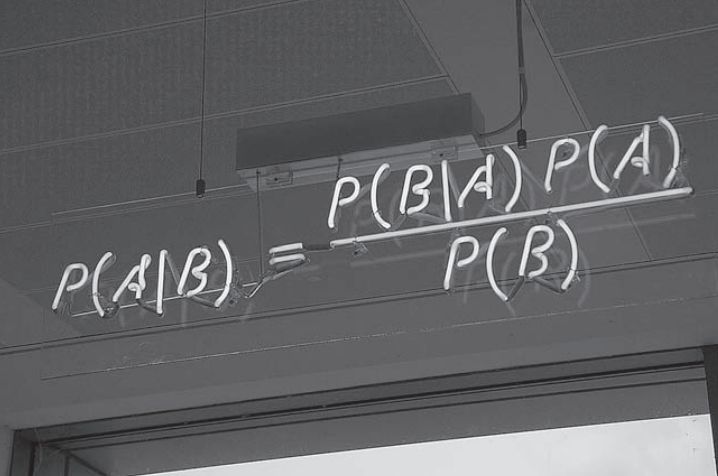
Теорема Байеса гласит, что

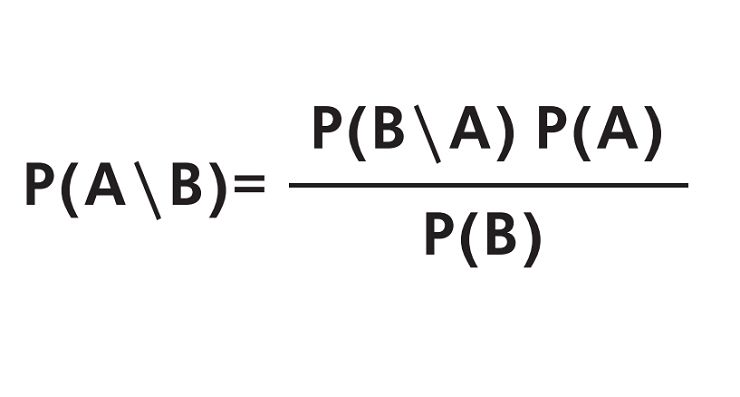
где Р — вероятность.

Известно, что Гитлер был вегетарианцем. Возможно, есть связь между деспотизмом и вегетарианством? Теорема Байеса поможет нам исследовать это, если мы соберем информацию о распространенности вегетарианства и деспотизма среди мировых лидеров прошлого и настоящего.

Предположим, мы выяснили, что 60% деспотов были вегетарианцами (Р = 0,6). Это наводит на мысль, что существует прочная связь между двумя явлениями. Однако, чтобы установить, так ли это, мы должны решить, какова доля вегетарианцев-деспотов. Давайте предположим, что мы выяснили, будто доля вегетарианцев среди мировых лидеров — 20% (Р = 0,2), и 5% мировых лидеров — деспоты (Р = 0,05).

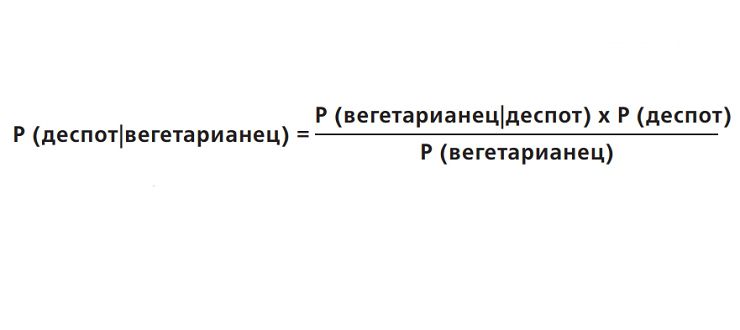
Подставим цифры:

Это полезный результат; хотя шанс любого конкретного деспота быть вегетарианцем — 60%, шанс любого лидера-вегетарианца быть деспотом — только 15%. Это по-прежнему несколько хуже, чем 5% вероятности, что любой лидер окажется деспотом, но не должно вести к тотальному запрету на то, чтобы вегетарианцы становились мировыми лидерами.

(Этот пример — продукт воображения и не направлен против вегетарианцев или мировых лидеров. Я вегетарианка, хотя и не мировой лидер.)

Когда все закончится?

Одно из применений байесовской вероятности (см. с. 240) — расчет вероятной даты конца человечества. Известный как Аргумент Судного дня, он впервые был предложен австралийским физиком Брендоном Картером в 1983 г. Он использовал довольно скромные цифры в 60 миллиардов людей, рожденных до настоящего момента (в 1983), чтобы рассчитать: 95% вероятности, что человечество не протянет дольше, чем еще 9120 лет (теперь уже меньше, чем 9100, так как несколько лет уже прошло с тех пор).