Геометрия Римана
В 1846 году Риман Георг Фридрих Бернхард поступил в Гёттингенский университет. Юный студент слушал лекции выдающегося немецкого математика Карла Гаусса. В Берлинском университете Бернхард Риман посещает лекции К. Якоби по механике и П. Дирихле по теории чисел. Знания полученных от этих гениальных ученых впоследствии будут развиты Риманом. В Гёттингенском университете Риман сотрудничал с талантливым физиком В. Вебером. Благодаря Веберу Риман заинтересовался проблемами математического естествознания. В 1851 Риман защитил докторскую диссертацию «Основы общей теории функций одной комплексной переменной». В 1857 становится профессором Гёттингенского университета. Лекции профессора Римана легли в основу ряда новых курсов таких, как математической физики, теории тяготения, электричества и магнетизма, эллиптических функций.
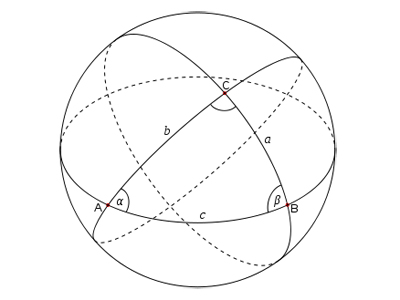
Сферический треугольник
Научно-исследовательские труды Бернхард Римана оказали огромное влияние на развитие математики в конце XIX и начале XX веков.
Уже в докторской диссертации Риманом были заложены основы геометрического направления теории аналитических функций. Выдающийся математик и геометр Риман ввел так называемые римановы поверхности, которые сыграли важную роль при исследовании многозначных функций. Более того, им была разработана теория конформных отображений, а также представлены основные идеи топологии, изучены условия существования аналитических функций внутри областей различного вида и многое другое.
Методы, разработанные Риманом нашли широкое применение в теории алгебраических функций и интегралов, по аналитической теории дифференциальных уравнений, в частности, уравнений, определяющих гипергеометрические функции, по аналитической теории чисел. К примеру, Риманом была указана связь распределения простых чисел со свойствами дзета-функции, а именно: с распределением её нулей в комплексной области — так называемая гипотеза Римана, однако ее справедливость ещё не доказана
В 1854 году в своей знаменитой лекции «О гипотезах, лежащих в основании геометрии» Риман дал общую идею математического пространства или «многообразия», включая функциональные и топологические пространства. Здесь Риман рассматривал геометрию как учение о непрерывных n-мерных многообразиях, то есть совокупностях любых однородных объектов. Обобщив результаты К. Гаусса по внутренней геометрии поверхностей, Риман сформулировал понятие линейного элемента, так называемого дифференциала расстояния между точками многообразия. Главным достижением ученого Римана стало создание новой геометрии.
Риманова геометрия — это раздел дифференциальной геометрии, объектом изучения которой, главным образом, являются римановы многообразия. Римановы многообразия — это гладкие многообразия с дополнительной структурой, римановой метрикой, то есть с выбором евклидовой метрики на каждом касательном пространстве, которая гладко меняется от точки к точке.Подразделом римановой геометрии является геометрия в целом, которая выявляет связь глобальных свойств риманова многообразия (к примеру, топология или диаметр) и его локальных свойств (к примеру, ограничений на кривизну).
Основными элементами трехмерной римановой геометрии являются точки, прямые и плоскости.
В римановой геометрии имеют место такие предложения: через каждые две точки проходит одна прямая, каждые две плоскости пересекаются по одной прямой, каждые две прямые, лежащие в одной плоскости, пересекаются (в одной точке), точки на прямой расположены в циклическом порядке (как и прямые, лежащие в одной плоскости и проходящие через одну точку). Таким образом, требования аксиом римановой геометрии, относящиеся конгруэнтности, обеспечивают свободные движения фигур по плоскости и в пространстве Римана, как на плоскости, так и в пространстве Евклида.
Метрические свойства плоскости Римана «в малом» совпадают с метрическими свойствами обыкновенной сферы, а именно: для любой точки плоскости Римана существует содержащая эту точку часть плоскости, изометричная некоторой части сферы; радиус R этой сферы — один и тот же для всех плоскостей данного пространства Римана. Число К = 1/R2 называется кривизной пространства Римана. Следует отметить, что, чем меньше К, тем ближе свойства фигур этого пространства к евклидовым.
«В целом» свойства плоскости Римана отличаются от свойств целой сферы в следующем: на плоскости Римана две прямые пересекаются в одной точке, а на сфере два больших круга, которые выступают как прямые в сферической геометрии, пересекаются в двух точках; прямая, лежащая на плоскости, не разделяет эту плоскость, таким образом, если прямая а лежит в плоскости a, то любые две точки плоскости a, не лежащие на прямой а, возможно соединить отрезком, не пересекая прямой а.
Таким образом, Риман построил вторую разновидность неевклидовой геометрии в противоположность геометрии Лобачевского.
Уникальные идеи и методы, предложенные Риманом открыли новые пути для развития математики и нашли применение в механике и физике. Развитию римановой геометрии послужило создание итальянскими учеными Риччи-Курбастро и Леви-Чивита тензорного исчисления.
