Системы счисления

Система счисления — это символический метод записи чисел, представление чисел с помощью письменных знаков.

Все существующие системы счисления делятся на три группы: позиционные, непозиционные и смешанные. Рассмотри более подробно каждую из них.

Неоспорим тот факт, что одним из высших достижений древней арифметики было открытие позиционного принципа представления чисел.

Первой из известных систем счисления была вавилонская шестидесятеричная система счисления, основанная на позиционном принципе. Возникла эта система счисления приблизительно во 2-ом тысячелетии до нашей эры.

Суть позиционных систем заключается в том, что один и тот же числовой знак, то есть цифра, в записи числа имеет различные значения в соответствии с местом (разрядом) расположения.

Значительно развили позиционную систему счисления индусы. Заслуга в создании десятичной системы счисления, которой пользуется вся современная человеческая цивилизация принадлежит именно индийским ученым математикам. Возникновение десятичной системы счисления тесно связано со счётом на пальцах. В Европу эта система была завезена купцами, которое позаимствовали ее у мусульманских народов.

Любая позиционная система счисления определяется некоторым числом b > 1, которое является основанием системы счисления. При этом это число должно быть таким, что b единиц в каждом разряде объединяется в одну единицу следующего по старшинству разряда. Подобная система счисления называется b-ричной.

Целое число x в b-ричной системе счисления представляется как конечная линейная комбинация степеней числа b:

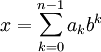
, где a_k — целые числа, называемые цифрами, удовлетворяющие неравенство 0 <= a_k < b.

В подобной записи каждая степень b^k называется b-ричным разрядом. Старшинство разрядов и соответствующих цифр определяется значением показателя k. Как правило, для числа x не равного нулю требуют, чтобы старшая цифра a_{n − 1} в b-ричном представлении x была также ненулевой. В таком случае число x записывают в виде последовательности его b-ричных цифр, перечисляемых по убыванию старшинства разрядов слева направо:

Приведем пример записи числа сто три в десятичной системе счисления:

В настоящее время существует несколько разновидностей позиционных систем счисления. Среди них наиболее употребляемыми являются:

• 1 — единичная система счисления. Часто это систему не рассматривают как позиционную. Представляет собой положительную суммарную целочисленную систему счисления с основанием равным 1. Единичная система счисления является древнейшей системой счисления в истории человечества. К примеру, счёт на пальцах, зарубки, узелки «на память» и др.;
• 2 — двоичная система счисления с основанием 2. Натуральные числа записываются в виде двух символов 0 и 1. Подобная система счисления используется в цифровых устройствах, в дискретной математике, информатике, программировании, поскольку является наиболее простой;
• 3 — троичная система счисления с основанием 3. Имеет две разновидности: симметричная (1-0-1) и несимметричная (0-1-2). Используется в цифровой электронике.
• 4 — четверичная система счисления, используется в вычислительной технике[1],
• 10 — десятичная система счисления, с целочисленным основанием 10. Самая распространенная система счисления в мире. Для записи чисел используются арабские цифры.
• 12 — двенадцатеричная система счисления (счёт дюжинами), использует цифры от 0 до 9 и латинские буквы А и В.
• 16 — шестнадцатеричная система счисления, широкое применение нашла в в программировании и шрифтах. Используются цифры от 0 до 9 и латинские буквы от А до F (для обозначения цифр от 0 до 15).
• 60 — шестидесятеричная система счисления, с целочисленным основанием 60. Используется с древних времен для представления измерения времени, измерения углов и, в частности, координат, долготы и широты.

Кроме положительных позиционных систем счисления существуют системы с отрицательными основаниями, которые называются нега-позициоонными. Имеют две разновидности: нега-двоичная и нега-десятичная система счисления.

Крайне редко пользуются позиционными системами счисления с дробными основаниями.