Задача о перемещении дивана

Те, кому приходилось передвигать мебель в своей квартире или хотя бы присутствовать при этом, наверняка сталкивались с весьма традиционной проблемой: шкаф или диван, которые должны быть передвинуты в другую комнату, никак не могут «протиснуться» в нужное место по «извилистому» коридору. Можно предположить, что знаменитая задача о перемещении дивана, сформулированная в 1966 году, родилась в голове канадского математика Мозера именно в тот момент, когда он пытался переставить мебель.

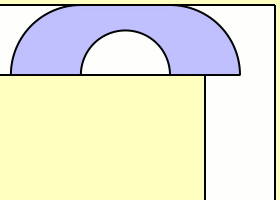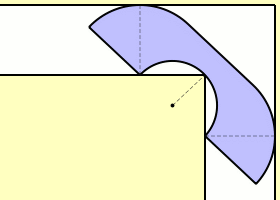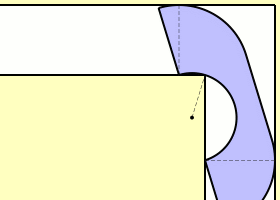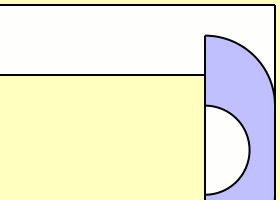
Представьте, что вы имеете коридор, который изгибается в форме буквы Г (он образован двумя небольшими коридорчиками, образующими прямой угол), через который необходимо «протащить» диван или стол (выражаясь сухим языком математики — «жесткое тело наибольшей площади А» — константы дивана). В некоторых подобных задачах через канал такого же вида необходимо провести корабль или баржу. Каким же образом необходимо поступить в данном случае?

Математики, занимающиеся решением этой задачи, начинали с того, что проводили за угол коридора полукруг единичного радиуса и оценивали константу дивана с нижней (π / 2 (1,570796327...) и верхней ( 2 sqr2 (2,828427124...) точек. Использование для решения задачи объекта, схожего с телефонной трубкой («трубка» представляла собой 2/4 кругов единичного радиуса, расположенных по сторонам от прямоугольника 1 x 4 / πс удаленным полукругом радиуса 2 / π), позволило математику Джону Хаммерсли значительно повысить оценку константы дивана снизу. Теперь она имела значение π / 2 + 2 / π (2,207416099...). В 90-х годах Джозеф Гервер, также «перемещавший диван», ограничил его восемнадцатью дугами окружностей и снова улучшил оценку константы дивана снизу. На этот раз она являлась 2,219531669... Однако, несмотря на все попытки решить задачу, нахождение точного значения константы дивана до сих пор не увенчалось успехом, в связи с чем эта «головоломка» объявлена нерешенной математической проблемой.