Магический квадрат
Одной из самых загадочных и популярных математических «головоломок» является знаменитый магический (волшебный) квадрат, который представляет собой табличку с равным количеством столбцов и строк, особенность которой заключается в том, что суммы чисел каждой строки, каждого столбца и каждой диагонали равны — это число называется «магической константой». Классические магические квадраты могут быть нормальными (используются целые числа от 1 и до n2), построенными для всех порядков, кроме второго, а также ассоциативными (сумма двух чисел, расположенных с соблюдением симметрии относительно центра квадрата равна n2 + 1). В том случае, если в «магии» задействованы только числа строк и столбцов, квадрат становится полумагическим.
Помимо классических, существуют нетрадиционные магические квадраты, самым известным из которых считается дьявольский (пандиагональный) магический квадрат. Особенность этого квадрата заключается в том, что к числам основных диагоналей добавляются еще и ломаные, т.е. те диагонали, которые, достигнув края, продолжаются параллельно первому отрезку от противолежащего края квадрата.
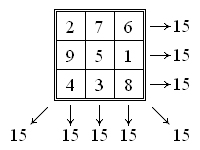
Если верить древнекитайской легенде, то первый магический квадрат Ло Шу, содержащий три строки и три столбца, числа которых в сумме составляли 15, был начертан на панцире священной черепахи, обитающей в водах Желтой реки. В Индии известен свой древнейший (XI века) магический квадрат, считающийся «дьявольским», сумма магических чисел которого равна 34. В Европе магический квадрат появился лишь в Средние века благодаря византийскому писателю Мосхопулосу, однако вся слава европейских волшебных квадратов досталась А. Дюреру, который первым придумал и изобразил его в своей гравюре «Меланхолия». Квадрат Дюрера в сумме 34 дает не только по вертикали, горизонтали и по диагонали: Дюрер пошел намного дальше — малые квадраты, составленные из четырех клеточек, расположенных по углам большого, квадрат из четырех клеточек в центре, сумма чисел в угловых клетках, квадраты, имитирующие «ход коня» и пр. — все дает в сумме 34. XYI век добавил в копилку «магии» и астрологии квадраты от 3 до 9 порядков, автором которых стал астролог Корнелий Генрих Агриппа. Благодаря ему магический квадрат с тех пор и поныне является символом магов и чародеев. Последние магические квадраты были построены в начале XX века Генри Дьюдени, Аланом Джонсоном (ими были созданы нетрадиционные магические квадраты, в которых используются не только натуральные числа) и Дж.Манси, который, за небольшим исключением, использовал последовательные простые числа.
Легко ли построить магический квадрат? Ученые считают, что, возможно, существует общий метод, зная который, достаточно просто создать любой магический квадрат, однако, к сожалению, он неизвестен, но, тем не менее, широко распространены частые схемы, авторами которых стали известные математики (Ф.де ла Ир, Л.Эйлер), один из которых — французский геометр А.де ла Лубера — предлагает строить магические квадраты пятого порядка (5×5) следующим образом. После того, как центр верхней строки заняло число 1, все натуральные числа помещаются по порядку снизу вверх в клетки диагоналей справа налево. Достигнув верха квадрата (клетки, соседствующей с единицей), необходимо заняться заполнением диагонали, которая берет начало от нижней клеточки следующего столбца. Оказавшись в пятой клетке второго ряда снизу, заполняется числами диагональ, следующая от первой клетки средней строки. После того, как будет заполнена последняя клетка верхней строки, необходимо спуститься на нижнюю строку и подобным образом продолжить построение магического квадрата.