Натуральные числа

Понятие натуральные числа возникло естественным образом при счете. Перечисляя или исчисляя человек еще в древности дал определение натуральных чисел.

Таким образом, числа 1, 2, 3, 4, 5, ..., использующиеся при счете предметов или для указания порядкового номера того или иного предмета (среди однородных предметов), называют натуральными. Натуральное число в десятичной системе счисления записывается с помощью цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Надо помнить, что отрицательные и нецелые числа — натуральными числами не являются.

Для обозначения множества всех натуральных числе пользуются знаком N.

В бесконечном множестве натуральных чисел для любого натурального числа найдется другое натуральное число, которое больше его.

Исходя из теории множеств, единственным объектом для построения любых математических систем является множество.

Введение натуральных чисел, согласно определению множества, выполняется по двум правилам:

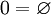
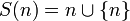
Такие числа, называются ординальными.

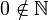Интересно узнать, что в русской математической традиции ноль исключается из числа натуральных чисел , а множество натуральных чисел с нулем обозначается как N₀.

Если ноль включают в ряд натуральных чисел, то множество записывается следующим образом: N, а без нуля как N^*.

Над натуральными числами можно проводить ряд арифметических операций. Рассмотрим основные из них.

---

Натуральные числа можно использовать для счёта (одно яблоко, два яблока и т. п.).

Операции, не выводящие результат из множества натуральных чисел, называются замкнутыми. К замкнутым арифметическим операциям относятся:

• Сложение. Слагаемое + Слагаемое = Сумма.
• Умножение. Множитель * Множитель = Произведение.
• Возведение в степень. a^b, где a — основание степени и b — показатель степени. Если основание и показатель натуральны, то степень будет являться натуральным числом.

К основным свойствам сложения и умножения натуральных чисел относятся:

• переместительное свойство сложения: a + b = b + a;
• сочетательное свойство сложения: (a + b) + c = a + (b +c);
• переместительное свойство умножения: ab = ba;
• сочетательное свойство умножения: (ab)c = a(bc);
• распределительное свойство умножения относительно сложения: a(b + c) = ab + ac.

Результатом сложения и умножение двух натуральных чисел всегда является натуральное число.

К дополнительным арифметическим операциям над натуральными числами относятся:

• Вычитание. Уменьшаемое — Вычитаемое = Разность. При этом Уменьшаемое должно быть больше Вычитаемого или равно ему (в том случае, если считать 0 натуральным числом).
• Деление. Делимое / Делитель = Частное (Остаток). Частное p и остаток r от деления a на b определяются так: a = p * b + r, причём 0 <= r < b. Следует заметить, что последнее условие запрещает деление на ноль, потому что тогда a можно представить в виде a = p * 0 + a, то есть можно было бы считать частным 0, а остатком = a.

Если m, n, k натуральные числа, то при m — n = k говорят, что m — уменьшаемое, n — вычитаемое, k — разность;

При m : n = k говорят, что m — делимое, n — делитель, k — частное.

К основным признакам делимости натуральных числе относятся:

• В том случае, если каждое слагаемое делится на некоторое число, то и сумма делится на это же число.
• Когда в произведении хотя бы один из множителей делится на некоторое число, то и произведение делится на это число.
• Натуральное число делится на 2 лишь в том случае, когда последняя цифра делится на 2.
• Натуральное число делится на 5 тогда, когда его последняя цифра либо 0, либо 5.
• Натуральное число делится на 10 в том случае, если его последняя цифра 0.
• Натуральное число, состоящее не менее из трех цифр, делится на 4 только тогда, когда делится на 4 двузначное число, образованное последними двумя цифрами заданного числа.
• Натуральное число делится на 3 только тогда, когда сумма его цифр делится на 3.
• Натуральное число делится на 9 только тогда, когда сумма его цифр делится на 9.