Рациональные числа
От латинского слова ratio — отношение, деление, дробь происходит математический термин рациональное число или рациональная дробь.
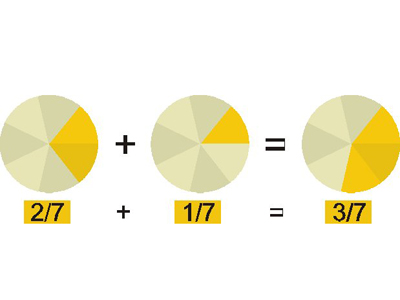
Суммирование дробей
Множество рациональных чисел принято обозначать Q. Наиболее точная графическая запись рациональных чисел такова: 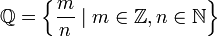 .
.

Нумерация рациональных чисел
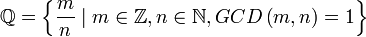 , где GCD (m, n)— наибольший общий делитель чисел m и n. Если он равен единице, то это гарантирует взаимную простоту«числителя и знаменателя, что в свою очередь обуславливает несократимость дроби m/n.
, где GCD (m, n)— наибольший общий делитель чисел m и n. Если он равен единице, то это гарантирует взаимную простоту«числителя и знаменателя, что в свою очередь обуславливает несократимость дроби m/n.Дробь, у которой модуль числителя меньше модуля знаменателя называется правильной. Дробь, не являющаяся правильной относится к неправильным.
Приведем пример, дроби 3/5, 7/8, и 1/2 — правильные дроби, а дроби 8/3, 9/5 и 2/1 — неправильные дроби.
Целое число и правильная дробь называется смешанной дробью, представляющая собой сумму числа и дроби. К примеру, 2 3/7 = 2 + 3/7 = 14/7 + 3/7 = 17/7.
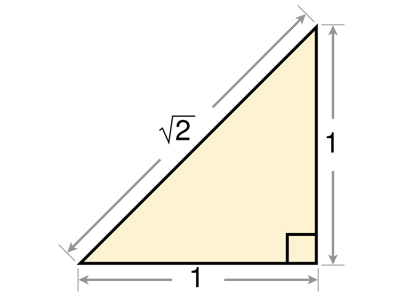
Гипотенуза такого треугольника не выражается никаким рациональным числом
К основным свойствам рациональных чисел относятся следующие:
- Упорядоченность. Для любых рациональных чисел a и b существует правило упорядочения, дающее возможность однозначно идентифицировать между ними одно из трёх отношений:» < », « > «или» = «. Точная формулировка этого правила такова: два неотрицательных числа a = ma/naи b = mb/nbсвязаны тем же отношением, что и два целых числа manb и mbna; два неположительных числа a и b связаны тем же отношением, что и два неотрицательных числа |b|и |a|; если же вдруг a неотрицательно, а b — отрицательно, то a > b.
- Операция сложения. Любые рациональные числа a и b подчиняются правилу суммирования, которое ставит им в соответствие некоторое рациональное число c, которое называется суммой чисел a и b и обозначается (a + b). Процесс поиска числа с называется суммированием.
Правило суммирования выглядит следующим образом: ma/namb/nb = (manb + mbna) / nanb. - Операция умножения. Для любых рациональных чисел a и b существует справедливо правило умножения, которое ставит им в соответствие некоторое рациональное число c. Здесь число c называется произведением чисел a и b и обозначается (ab). Процесс отыскания числа с называется умножением. Правило умножения имеет следующий вид: ma/namb/nb = (mamb)/(nanb).
- Транзитивность отношения порядка. Для любой тройки рациональных чисел a, b и c в случае, если a меньше b, а b меньше c, то a меньше c. Когда a равно b, а b равно c, то a равно c. Т.е. (a < b & b < c => a < c) & (a = b & b = c => a = c)
- Коммутативность сложения. Всем известное правило: от перемены мест рациональных слагаемых сумма не меняется. Т.е. a + b = b + a.
- Ассоциативность сложения. На результат сложения не влияет порядок сложения трех рациональных чисел. Т.е. (a + b) + c = a + (b + c).
- Наличие нуля. При суммировании любых рациональных чисел рациональное число 0 сохраняет их. a + 0 = a.
- Наличие противоположных чисел. Любое рациональное число имеет противоположное рациональное число, при суммировании с которым даёт 0. a + (-a) = 0.
- Коммутативность умножения. Произведение рациональных чисел от перемены мест рациональных множителей не меняется. ab = ba.
- Ассоциативность умножения. На результат перемножения трех рациональных чисел порядок не влияет. (ab)c = a(bc).
- Наличие единицы. Наличие рационального числа 1 при умножении сохраняет любое другое рациональное число. a1 = a.
- Наличие обратных чисел. Любое рациональное число имеет обратное рациональное число, при умножении на которое даёт 1. aa-1 = 1.
- Дистрибутивность умножения относительно сложения. Операция умножения согласуется с операцией сложения на основе распределительного закона: (a + b)c = ac + bc.
- Связь отношения порядка с операцией сложения. Одно и то же рациональное число можно прибавить и к левой и правой частям рационального неравенства. a < b => a + c < b + c.
- Связь отношения порядка с операцией умножения. Одно и то же положительное рациональное число можно умножать на левую и правую части рационального неравенства. c > 0 & a < b => ac < bc.
- Аксиома Архимеда гласит, что каково бы ни было рациональное число a, можно взять столько единиц, что их сумма превзойдёт a.
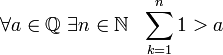
Кроме основных шестнадцати свойств, присущих рациональным числам существуют и другие, которые могут быть выведены из приведенных свойств. Дополнительных свойств рациональных чисел очень много.
