Григорий Яковлевич Перельман и его вклад в науку
Математика — самая абстрактная из наук. Но в то же время именно она служит тем мощным инструментом, с помощью которого можно описать любое явление во Вселенной, вне зависимости от того, какой наукой оно изучается. И, несмотря на абстрактность, математика находит самое широкое применение в практической деятельности, мало того — в свое время разные ее разделы создавались тогда, когда появлялась необходимость. Надо было считать предметы и измерять землю — были придуманы арифметика и элементарная геометрия. Возникла необходимость более сложных вычислений — появились алгебра и другие разделы. Ньютону для доказательства теории всемирного тяготения не хватало существовавшего в XVII веке математического аппарата, и он «выдумал» интегральное и дифференциальное исчисление. После Ньютона многими учеными было создано большое количество самых разных разделов и направлений математики, и почти все они имели и имеют практическое значение.

А почему математика абстрактна? Да все просто — ведь даже таких привычных нам понятий, как «число» и «математическое действие», в природе не существует. Они выдуманы человеком, который, единственный из всех живых существ на Земле, может мыслить абстрактно. Чтобы понять весь смысл этого, нужно оглядеться вокруг и убедиться — почти все, что придумано человеком, имеет свои аналоги в природе. А вот числа (как и колеса) — нет. Поэтому математика — это игры разума в чистом виде, однако здесь существует риск перейти грань между ней и философией и отдалиться от основной темы.
В математике есть направление топология — пожалуй, одно из самых абстрактных, хотя и оперирует вещами вполне реальными и имеющими практическое значение. В топологии изучается пространство, а точнее — его свойства при различных видах деформации.
Однако для топологии важны не метрические характеристики пространства (как, например, в геометрии, где имеют значение точные измерения длин, площадей, объемов и т. д.), а пространство само по себе.
Топология зародилась в конце XIX века, а в начале следующего уже стала самостоятельной научной дисциплиной. Одним из ее основоположников был Анри Пуанкаре — великий французский математик и физик, внесший огромный вклад в развитие целого ряда научных дисциплин. Именно он был автором математической гипотезы, выдвинутой в 1904 году и ставшей одной из семи задач тысячелетия.

Гипотеза Пуанкаре ждала своего доказательства почти целый век. Решил ее русский математик Григорий Перельман — и в одночасье стал знаменит на весь мир (справедливости ради стоит заметить, что этому поспособствовали и другие причины). Доказавшему гипотезу были обещаны миллион долларов (от которого Перельман отказался) и, конечно же, слава и почет в мировом научном сообществе. Что же представляет собой эта задача на миллион и почему она стала одной из задач тысячелетия?
Немного о топологии
В конце XIX века некоторые математики, в том числе и Анри Пуанкаре, занимались проблемами недавно сформировавшейся топологии. Уже были установлены основные законы этой дисциплины, которые, однако, относились только к двумерным поверхностям.
Но для математиков и наш трехмерный мир слишком тесен, и Пуанкаре стало интересно, как ведут себя геометрические объекты в пространствах, в которых количество измерений более трех.
Для того чтобы немного прояснить ситуацию, нужно подробнее рассказать об измерениях, многомерных пространствах и объектах, существующих в этих пространствах.

Мы живем в трехмерном мире: у любого тела есть легко измеряемые длина, ширина и высота. Однако с точки зрения топологии в трехмерном пространстве существуют только двумерные объекты, а точнее — поверхности. Эта дисциплина рассматривает не объекты или физические тела — ей откровенно все равно, из чего состоит тело. Главное для математиков-топологов в прямом смысле слова лежит на поверхности — их интересуют только поверхности и их свойства при различных видах деформаций.
Если посмотреть на сферу (или на другое геометрическое тело) с точки зрения топологии, то она представляет собой замкнутую поверхность, обладающую всего двумя измерениями. Почему двумя? Да потому, что если поместить на поверхности сферы гипотетическое микроскопическое существо, то оно сможет перемещаться только по направлениям двух измерений, то есть вдоль поверхности сферы. Подпрыгивание или, наоборот, зарывание под поверхность сферы не считается, так как в этом случае происходит отрыв от поверхности, а топологии интересны, как мы помним, только сами поверхности, а не то, что их окружает.
В этом контексте даже земной шар обладает двумерной поверхностью, да и поверхность наших тел двумерна, как и вообще всех тел во Вселенной. Отсюда важное следствие: в пространстве с количеством измерений n (n = 3, 4, 5 и более) существуют поверхности с количеством измерений n – 1. То есть в трехмерном пространстве поверхности двумерны, в четырехмерном — трехмерны, в семимерном — шестимерны и т. д.
Представить себе трехмерную поверхность невозможно — наш мозг при всех попытках будет рисовать аналогии из привычного, трехмерного, мира, поэтому за многие десятилетия так и не удалось более или менее точно визуализировать объекты четырехмерного мира. Однако с помощью математического аппарата можно воссоздать (но только в числах и уравнениях) объекты практически с любым количеством измерений.
Итак, к концу XIX — началу XX века топологи уже многое знали о двумерных поверхностях, да и трехмерные были частично изучены. Однако Анри Пуан каре интересовало, действуют ли в многомерных пространствах законы, справедливые в трехмерном пространстве для двумерных поверхностей. Проще говоря, ученый хотел знать, можно ли многомерный куб (или любую другую фигуру) путем деформаций преобразовать в многомерную сферу так же, как это делается в нашем мире. Непонятно? Еще несколько объяснений — и все станет свои места.
Гипотеза Пуанкаре
Желание узнать свойства многомерных поверхностей Анри Пуанкаре выразил в гипотезе, сформулированной в 1904 году. В настоящее время она звучит следующим образом:
любое односвязное замкнутое трехмерное многообразие гомеоморфно трехмерной сфере.
Казалось бы, что что-то понять из этой формулировки невозможно, но это далеко не так, вникнуть в смысл гипотезы помогут несколько простых замечаний.

Термин «многообразие» означает объект, а точнее — поверхность. Топологи используют именно это понятие, и неспроста: оказывается, любую поверхность, даже самую сложную и многомерную, можно разбить на множество кусочков, свойства которых хорошо описываются привычной нам «плоской» евклидовой геометрией. Такое допущение значительно облегчает математические расчеты, поэтому в топологии рассматриваются не просто объекты и поверхности, а многообразия.
Один из ключевых моментов в гипотезе — так называемая связность. В топологии именно связность является главным свойством, определяющим отличия одних объектов от других.
Как бы удивительно это ни звучало, но для математика-тополога нет принципиальной разницы между шаром и кубом, футбольным мячом и Землей, кружкой и спасательным кругом.

Дело в том, что в топологии рассматриваются не физические объекты, обладающие массой, жесткостью (или, наоборот, эластичностью), твердостью и другими привычными для нас характеристиками, а само пространство и поверхности этих объектов. Но самое главное, что в топологии определяющими являются различные деформации этих поверхностей. Самый распространенный тип задач этой области математики сводится к поиску ответа на вопрос о том, как без разрывов, разрезов и склеек, а лишь посредством деформаций (сжимания, скручивания, растягивания) из одной поверхности получить другую.
Например, поверхность куба можно сжимать и растягивать так, что в конечном итоге получится сфера, а поверхность бублика легко (конечно же, с точки зрения математики) растягивается и приобретает форму чашки с ручкой.
Именно поэтому топологию часто называют математикой резинового листа —
ученые так выкручивают, растягивают и сжимают разные двумерные и многомерные поверхности, что остается только удивляться их мастерству.
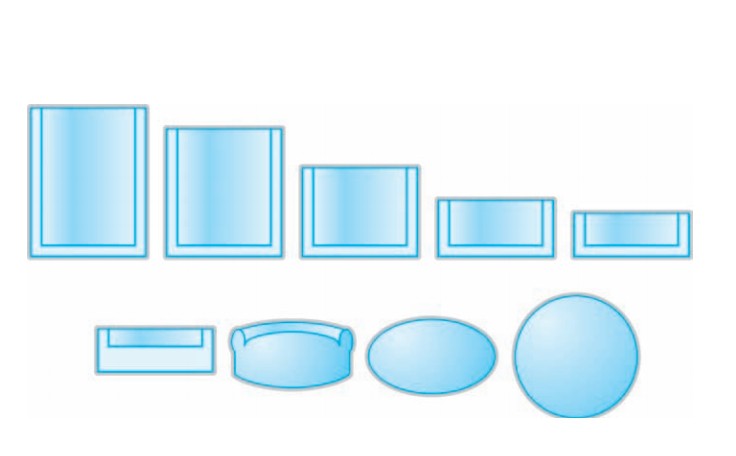
Если вникнуть в суть написанного, то можно прийти к выводу, что поверхности очень многих объектов, кажущиеся нам совершенно непохожими, с точки зрения математики одинаковы (то есть эквивалентны). Это иллюстрируют примеры деформаций куба в сферу и бублика в кружку.
А что будет, если попытаться преобразовать бублик в сферу? Ничего не будет, так как данная попытка нарушит главное правило топологии — шар получится только в случае разрезания и склеивания бублика.
Теперь уже легко понять, что главное отличие объектов и поверхностей в топологии кроется не в их формах, а в наличии или отсутствии дырок.
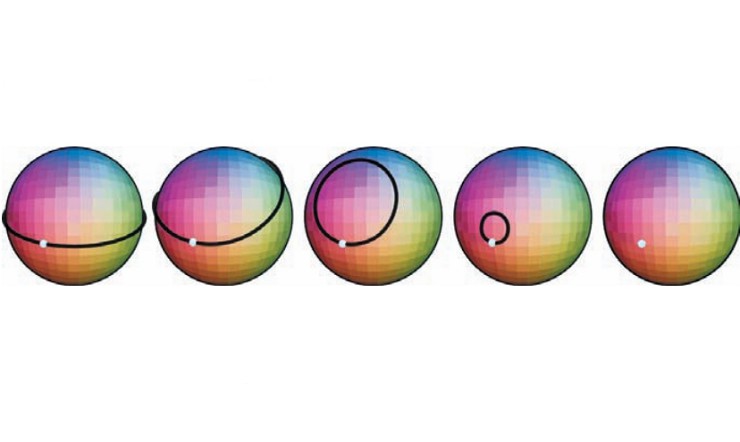
Поэтому для математиков все поверхности без дырок идентичны между собой, как эквивалентны друг другу и все поверхности с одной, двумя и большим количеством дырок.
Ученые не оперируют понятием «дырка» — слишком уж оно ненаучное. В топологии применяется термин «связность». Все объекты без дырок (например, сфера) являются односвязными, объекты с одной дыркой — двусвязными и т. д. Чтобы примерно представить, что такое связность, нужно взять тонкий резиновый шнур и обмотать его вокруг объекта, образуя петлю. Если сделать это на сфере, то возникает интересная ситуация — при стягивании петли она будет «сползать» с экватора сферы к ее полюсу, где сожмется в точку. При этом на сферу можно накинуть всего одну такую петлю (ее называют стягиваемой). Даже если и опоясать шар десятью подобными петлями, то каждая из них будет вести себя абсолютно одинаково, сжимаясь в точку.
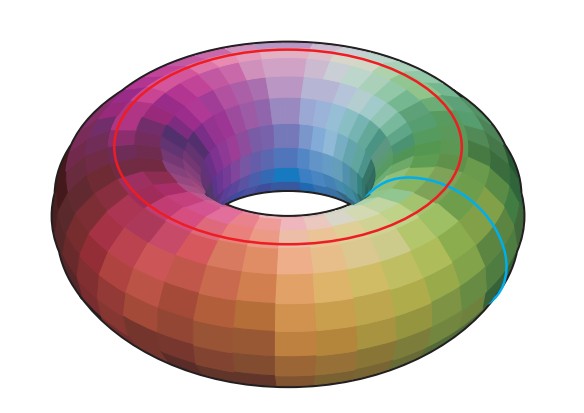
Если провести эксперимент с резиновой нитью на бублике (на математическом языке — торе), то результат будет иным. Во-первых, на тор можно накинуть две разные петли: одна будет проходить через отверстие и опоясывать тор поперек, а вторая станет располагаться по кругу, не проходя сквозь дыру.
И самое главное — ни одна из петель не может быть стянута в точку — для этого она должна либо разорваться сама, либо разорвать тор.
Осталось рассмотреть два таких понятия, как замкнутость многообразия и гомеоморфизм. О каждом из них уже было немного сказано, правда, они упоминались «не под своими именами». Замкнутым многообразием называется объект, поверхность которого не имеет краев. Ярким примером служит сфера — как ни крути, а у нее нет края. А гомеоморфизм — это и есть те самые деформации без разрезов и склеек, в процессе которых одна поверхность преобразуется в другую.
Все, что было только что рассмотрено в отношении двумерных поверхностей, в одинаковой степени относится и к поверхностям с любым количеством измерений. Однако не нужно забывать, что трехмерная сфера или трехмерный тор в четырехмерном пространстве совершенно не похожи на сферу и тор, которые мы привыкли наблюдать.
Теперь гипотезу Пуанкаре можно объяснить совсем просто: любая трехмерная поверхность без дырок может быть путем деформаций преобразована в трехмерную сферу. И эта простая по своей сути идея оказалась таким «крепким орешком», что целых 98 лет не могли найти ее строгого математического подтверждения, а когда решение все-таки было озвучено, оно еще четыре года проверялось математиками ведущих институтов мира.
Кое-что об истории и ошибках
Нужно сказать, что гипотеза Пуанкаре не сразу привлекла внимание математиков. Напротив, работа французского ученого, в которой и была сформулирована знаменитая задача, прошла незамеченной. Лишь спустя три десятка лет была сделана первая попытка найти доказательство — британский ученый Джон Уайтхед представил свой вариант решения гипотезы. И тогда даже показалось, что она доказана, но… именно показалось — Уайтхед сделал ряд ошибок, и гипотеза Пуанкаре так и осталась загадкой.
Однако вот что удивительно: допущенные неточности вошли в историю. Дело в том, что работа ученого положила начало новой теории многообразий (названной в его честь), которая сейчас имеет немалое научное и практическое значение.
Только после Уайтхеда ученые обратили внимание на гипотезу Пуанкаре и поднятую в ней проблему. И с тех пор математики уже не прекращали попыток найти доказательства. Однако на протяжении следующих шести с небольшим десятилетий успеха в этом направлении добиться так и не удалось.
Конечно, говорить о полной неудаче было бы некорректно. Гипотеза Пуанкаре была сформулирована только для трехмерных поверхностей, но мы уже знаем, что в топологии рассматриваются пространства с любым количеством измерений. Значит, данная гипотеза в общем случае может быть приложена к пространствам и поверхностям с любым количеством измерений. Поэтому математики искали ее доказательство не только для трехмерных, но и для многообразий с большим количеством измерений.
Нужно сказать, что в деле поиска решений задачи Пуанкаре для многомерных пространств были достигнуты отличные результаты. К 1982 году были найдены доказательства для поверхностей с количеством измерений от четырех (этот случай оказался одним из самых сложных, но именно он был решен первым) до семи и более. А вот исходный вариант гипотезы — для трехмерных поверхностей — оставался неприступным, и за него уже брались немногие.
Значительную роль сыграло несколько ученых, усилиями которых были созданы непонятные для неспециалистов, но важные для математики теории и инструменты. В частности, в 1980-х годах американский ученый Ричард Гамильтон наметил план доказательства гипотезы Пуанкаре с использованием математического инструмента, названного потоком Риччи.
Как раз основываясь на достижениях Гамильтона, наш гениальный соотечественник Григорий Яковлевич Перельман и вывел свое доказательство гипотезы, которое стало общепризнанным и прославило ученого.
Еще в 1992 году Григорий Перельман приехал в США (в то время он уже был известен в научных кругах), где прочитал цикл лекций и познакомился с Ричардом Гамильтоном. Ученые обменялись соображениями по поводу гипотезы Пуанкаре, и Перельман посчитал, что американский коллега близок к ее решению. Позже российский ученый периодически узнавал, как обстоят дела у Гамильтона, и убеждался, что тот так и не продвинулся в вычислениях.
Перельман продолжил работать над гипотезой, и спустя годы упорной работы в Интернете (2002 год) появились три его статьи, в которых фактически содержалось полное доказательство гипотезы Пуанкаре.
Научное сообщество заинтересовалось, а Перельман, в свою очередь, подлил масла в огонь, представив окончательное решение великой задачи. Однако только через четыре года стало ясно, что доказательство, над поисками которого билось несколько сотен профессионалов на протяжении века, наконец-то найдено. При этом оно отличается простотой и изяществом. И нужно заметить, что его проверкой на протяжении этих четырех лет занимались сразу три (!) группы ученых-математиков в разных университетах.
Кстати, а при чем здесь ошибки? При том, что во время поисков доказательства гипотезы Пуанкаре ошибся не только Уайтхед, но и еще ряд ученых, и все эти неточности привели к созданию десятков топологических теорий, задач, инструментов и даже отдельных направлений в науке.
О пространствах и Вселенной
Итак, в 2002 году великая гипотеза Пуанкаре была, наконец, доказана, и сделал это русский ученый Григорий Перельман.
Вокруг данной математической задачи всегда было много шуму, и любое, даже незначительное открытие вызывало немалый интерес. А почему гипотезе уделялось столько внимания и почему именно она стала одной из семи задач тысячелетия?
Для начала присутствует чисто математический интерес: ученые хотели знать, справедливы ли правила топологии, которые работают в трехмерном пространстве, в многомерных пространствах. Перельман доказал, что любая односвязная трехмерная поверхность (без дырок) гомеоморфна трехмерной сфере, то есть путем деформаций без разрезов и склеек может быть преобразована в эту самую сферу.
Но чисто математический интерес закончился тогда, когда стала развиваться космология — наука о Вселенной. Как могут быть связаны между собой абстрактная математическая гипотеза и самый большой из реально наблюдаемых нами объектов? Оказывается, связь самая прямая и доказательство гипотезы Пуанкаре имеет большое значение для науки о Вселенной.
Например, многолетние экспериментальные наблюдения и работы ученых дают основание считать, что пространство Вселенной не совсем плоско. Ее можно считать трехмерной сферой, которая фигурирует в гипотезе Пуанкаре.
В 1915 году выдающийся физик-теоретик Альберт Эйнштейн (с которым, кстати, у Анри Пуанкаре были весьма натянутые отношения из-за расхождения взглядов на природу Вселенной) представил общую теорию относительности, ставшую одной из первых космологических работ. В 1922-м наш соотечественник геофизик Александр Фридман высказал идею о нестационарной (расширяющейся) Вселенной, в которой теория относительности играла большую роль. И уже в то время ученые задались вопросом — в мире с каким пространством мы живем?
Вообще возможны два основных варианта: наше пространство либо плоско, либо искривлено. При этом искривление может быть двух видов — положительным или отрицательным. Положительной кривизной обладает, например, сфера, а отрицательной — гиперболоиды, седловые поверхности (похожие на седло) и другие геометрические тела, то есть вопрос о том, каким является пространство Вселенной, напрямую связан с топологией.
Многолетние экспериментальные наблюдения и работы ученых дают основание считать, что пространство Вселенной не совсем плоско и может приблизительно считаться той самой трехмерной сферой, фигурирующей в гипотезе Пуанкаре. Таким образом, абстрактная задача, описывающая не существующие в природе объекты (а если сказать точнее — не существующие для человеческого восприятия, мы до сих пор не знаем, есть ли дополнительные измерения в нашем мире, но наука говорит, что, скорее всего, имеются), стала одной из решающих в космологии.
Доказательство гипотезы Пуанкаре имеет большое значение для теории Большого взрыва, утверждающей, что 13,7 миллиарда лет назад вся наша Вселенная помещалась в точке бесконечно малого объема.
Чтобы понять эту связь, нужно вспомнить об эксперименте с резиновой нитью на двумерной сфере — она, как мы знаем, там может быть затянута в петлю точечных размеров. Но здесь есть и другое следствие: в точку может стянуться не только петля на поверхности сферы, но и сама сфера: ведь ее поверхность способна деформироваться, сжимаясь до минимальных размеров, но при этом оставаясь сферой.
Это справедливо и применительно к трехмерной сфере — гипотетический гипершнур может сам стянуться в точечную петлю на ее поверхности и стянуть в точку саму сферу. А если наша Вселенная будет представлена такой трехмерной сферой, то ей ничто не мешает иметь как бесконечно большие, так и бесконечно малые объемы, то есть она может обратиться в точку.
Однако топология и гипотеза Пуанкаре имеют отношение не только к самым большим расстояниям, но и к самым маленьким. В настоящее время одной из ведущих и перспективных в физике является теория струн.
Она способна нормально «работать» и объяснять процессы и явления нашего мира только при допущении, что пространство не трехмерно, — сейчас считается, что измерений не менее одиннадцати.
Но все они заметны только на субъядерном уровне, то есть мы не сможем увидеть их ни при каком желании. Зато элементарные частицы буквально живут в этих измерениях, поэтому достижения топологии в целом и доказательство гипотезы Пуанкаре в частности помогают познать законы, царящие в микромире. Все это может приблизить физиков к заветной цели — созданию единой Теории Всего, название которой говорит само за себя.
Кроме того, четвертое измерение пространства становится заметным и при скоростях, близких к скоростям света (около 300 тысяч км/с). То есть гипотеза Пуанкаре проникает и в релятивистскую физику, объясняя свойства пространства при околосветовых скоростях и колоссальных силах гравитации (вблизи черных дыр или нейтронных звезд).
Тем самым доказанная гипотеза Пуанкаре (хотя с 2002 года ее уже можно назвать теоремой) на строгом математическом языке лишний раз говорит о справедливости теории Большого взрыва, помогает понять структуру пространства в релятивистской физике и вносит некоторую ясность в фундаментальные теории строения мира. Сам Анри Пуанкаре в 1904 году вряд ли мог догадываться о том, какой смысл заложен в сформулированной им задаче, ведь тогда и космология пребывала в зачаточном состоянии. А вот Григорий Перельман понимал, в чем ценность гипотезы.

Сейчас доказательство гипотезы Пуанкаре неоднократно проверено и признано справедливым. И трудно найти человека, не слышавшего о русском ученом Перельмане, гипотезе Пуанкаре и миллионе долларов. К сожалению, гораздо более широкую известность получил отказ математика от баснословной суммы награды, а не само доказательство.
Краткая биография
Григорий Яковлевич Перельман родился 13 июня 1966 года в Ленинграде. Отец был инженером-электриком, мать — учителем математики. Одаренность Григория проявилась уже в детстве, с 5-го класса он занимался в математическом центре для одаренных детей, побеждал в математических олимпиадах разного уровня.

В 1982 году занял первое место в международной олимпиаде в Будапеште, в том же году без экзаменов принят на математико-механический факультет Ленинградского государственного университета. После окончания вуза поступил в аспирантуру при Ленинградском отделении Математического института им. В. А. Стеклова РАН, после защиты кандидатской диссертации остался работать в институте.
С 1992 по 1996 год жил и работал в США, после снова вернулся в институт им. В. А. Стеклова. Ученый активно занимался многими математическими проблемами, но особенно его интересовала топология.
В 2002-м Перельман опубликовал в Интернете несколько статей, в которых была доказана гипотеза Пуанкаре. В конце 2005-го ученый неожиданно для всех покинул институт и полностью отстранился от математики.
В 2006 году доказательства Перельмана были проверены рядом ученых, в итоге ему была присуждена медаль Филдса. В 2010-м ученому присуждена премия Математического института Клэя (1 млн долларов). Однако Григорий Перельман отказался от всех наград.
В настоящее время гениальный математик, потративший много лет на поиск доказательства гипотезы Пуанкаре, ведет замкнутый образ жизни, не общается с журналистами и полностью отошел от науки.
