Непозиционные системы счисления

Отличительная особенность непозиционных систем счисления заключается в том, что величина, которую обозначает цифра, не зависит от положения в числе. Таким образом, система может накладывать ограничения на положения цифр. К примеру, расположение цифр в порядке убывания или возрастания.

Существует несколько видов непозиционных систем счисления. Рассмотрим более подробно каждую из них.

Первой разновидностей непозиционных систем счисления является биномиальная система счисления. В основе подобной системы счисления лежит представление, использующее биномиальные коэффициенты:

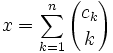
, где 0 <= c₁ < c₂ < ... < c_n.

Ко второму виду непозиционных систем счисления относится греческая система счисления. Также известная как ионийская греческая непозиционная система счисления в качестве символов для счета использует греческие буквы и специальные символы, к примеру ς (стигма), Ϙ (копа) и Ϡ (сампи) и др..

Подобная система счисления способствовала ранней стабилизации греческого алфавита.

Следующей разновидностью является римская система счисления. Она являет собой образец непозиционной системы счисления, в которой в качестве цифр использовались латинские буквы.

Каноническим примером фактически непозиционной системы счисления является римская, в которой в качестве цифр используются латинские буквы:

• I = 1,
• V = 5,
• X = 10,
• L = 50,
• C = 100,
• D = 500,
• M = 1000

Таким образом, запись сложения в римской системе счисления имела следующий вид: I+I = II (то есть, 1 + 1 = 2). Следовательно, символ I обозначает 1 независимо от места в числе.

Однако стоит заметить, что римская система все же полностью не является непозиционной. Приведем пример: IV = 4, в то время как, VI = 6.

Рассмотрим систему остаточных классов (СОК), в которой представление числа основано на понятии вычета, заимствованное на китайской теореме об остатках. Система остаточных классов определяется набором взаимно простых модулей (m₁, m₂,...,m_n) с произведением M = m₁m₂...m_n поэтому, каждому целому числу x из отрезка [0,M − 1] соответствует определенный набор вычетов (x₁, x₂,...,x_n), где x = x₁ (mod m₁); x = x₂ (mod m₂);...;x = x_n (mod m_n);

Китайская теорема об остатках обуславливает однозначность представления для чисел отрезка [0, M − 1].

В системе остаточных классов основные арифметические операции (сложение, вычитание, умножение, деление) выполняются покомпонентно, в том случае, если известно, что результат является целочисленным и находится на отрезке [0,M − 1].

Главный недостаток системы остаточных классов заключается в ограниченной возможности представления количества чисел, а также отсутствие результативных алгоритмов для сравнения. В системе остаточных классов сравнение, как правило, осуществляется путем перевода аргументов из системы остаточных классов в смешанную систему счисления по основаниям (m₁, m₁m₂,...,m₁m₂...m_n-1).

Еще одной разновидностью непозиционных систем является Система счисления Штерна-Броко. Подобная система счисления основывается на особом способе записи положительных рациональных чисел (дерево Штерна-Броко).