Дифференциальная геометрия
Дифференциальная геометрия — это один из разделов геометрии, в котором изучаются свойства кривых, поверхностей и других геометрических многообразий с помощью методов математического анализа, в частности — дифференциального исчисления.
Возникла и развивалась дифференциальная геометрия вместе с математическим анализом, который сам в действительности базируется на геометрии. основные геометрические понятия легли в основу соответствующий терминов анализа. К примеру, понятие площади и объема предшествовало понятию интеграл.
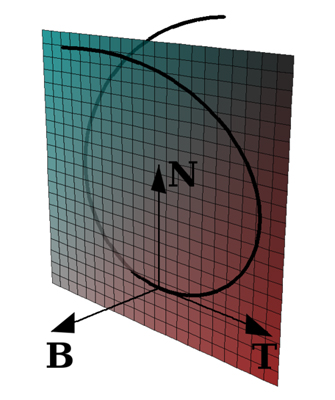
В точке кривой построены векторы касательной (T), главной нормали (N) и бинормали (B). Показана также соприкасающаяся плоскость, содержащая касательную и главную нормаль
Зародилась дифференциальная геометрия в XVIII веке. Ее появление связано с именами выдающихся математиков того времени Эйлера и Монжа. Первое сводное сочинение по теории поверхностей была написано в 1795 году Монжем «Приложение анализа к геометрии».
В 1827 Гаусс опубликовал работу «Общее исследование о кривых поверхностях», в которой изложил основы теории поверхностей в её современном виде. С этого момента дифференциальная геометрия получила официальный статус самостоятельной отрасли математической науки.

Полигональное приближение кривой
Научно-исследовательские работы по дифференциальной геометрии К. Гаусса (1777-1855гг.), Г. Дарбу (1842-1917гг.), Л. Бианки (1856-1928гг.) и Л.Эйзенхарта (1876-1965гг.) были посвящены, главным образом, свойствам, проявляющимся в малой окрестности обычной точки многообразия. Предмет этих исследований стал сутью так называемой дифференциальной геометрии «в малом». Начиная с 1930-х годов, исследования математиков были направлены, прежде всего, на изучение взаимосвязей между дифференциальной геометрией малых окрестностей и «глобальными» свойствами всего многообразия. Эта теорию получила название дифференциальной геометрией «в целом».
Важную роль в развитии геометрии, и дифференциальной геометрии, в частности, сыграло открытие неевклидовой геометрии. В лекции «О гипотезах, лежащих в основаниях геометрии», прочитанной Риманом в 1854 году, были сформулированы основы новой геометрии. впоследствии эта геометрия стала носить имя своего создателя. Сегодня риманова геометрия является наиболее развитой частью дифференциальной геометрии.
Геликоид
В «Эрлангенской программе» 1872 года Клейн изложил теоретико-групповую точку зрения на геометрию. Согласно Клейну, геометрия — это учение об инвариантах (то есть об неизменных величинах) групп преобразований. Применительно к дифференциальной геометрии это учение было развито Картаном, который создал теорию пространственно-проективной и аффинной (родственной) связности.
Следует отметить, что дифференциальная геометрия и топология являются смежными разделами математики. Однако топология значительно более молодой раздел, который начал развиваться лишь в начале XX века.
Наиболее фундаментальная из известных взаимосвязей между топологией и дифференциальной геометрией устанавливается теоремой Гаусса — Бонне, которая утверждает, что для обычных замкнутых поверхностей
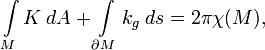
где интеграл берется по всей поверхности, K — гауссова кривизна поверхности M, kg — геодезическая кривизна δM, a χ(M) - эйлерова характеристика M. На произвольные замкнутые римановы пространства этот результат был распространен в 1943 К.Аллендёрфером и А.Вейлем.
Надо сказать, что дифференциальная геометрия также как и вся геометрия подразделяется на несколько основных отраслей. К ним относятся:
- Метрическая дифференциальная геометрия
- Дифференциальная геометрия кривых.
- Проективная геометрия.
- Аффинная геометрия.
- Конформная дифференциальная геометрия.
- Риманова геометрия.
- Симплектическая топология.
- Теория поверхностей.
- Финслерова геометрия.
Первоначально дифференциальная геометрия занималась изучением свойств кривых поверхностей в обычном пространстве, в настоящее время в область ее изучения вошли многообразия любого числа измерений, которые могут быть, а могут и не быть подпространствами евклидова пространства.
