Стохастические фракталы

Третьей крупной разновидностью фракталов являются стохастические фракталы, которые образуются путем многократных повторений случайных изменений каких-либо параметров. В результате итерационного процесса получаются объекты очень похожие на природные фракталы — несимметричные деревья, изрезанные лагунами береговые линии островов и многое другое. Двумерные стохастические фракталы используются преимущественно при моделировании рельефа местности и поверхности моря.

---

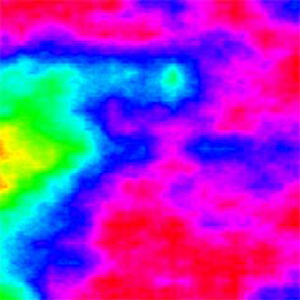
Плазма

Наиболее яркими примерами стохастических фракталов являются:

• Траектория броуновского движения на плоскости и в пространстве. А также граница траектории броуновского движения на плоскости. Следует отметить, что в 2001 году известные математики Лоулер, Шрамм и Вернер доказали предположение Б. Мандельборта о том, что размерность границы броуновского движения на плоскости равна 4/3.
• Эволюции Шрамма-Лёвнера — конформно-инвариантные фрактальные кривые, возникающие в критических двумерных моделях статистической механики. Наглядным примером этой разновидности стохастических фракталов является модель Изинга и перколяции.
• Разнообразные виды рандомизированных фракталов. Это такие фракталы, которые образуются с помощью рекурсивной процедуры, в которую на каждом шаге вводится случайный параметр. Очень часто эту разновидность фракталов используют в компьютерной графике для изображения плазмы.

На так давно в изобразительном искусстве сформировалось новое направление — фрактальная монотипия или стохатипия, целью которых является получение изображения случайного фрактала.