Топология

Лента Мёбиуса — поверхность с одной стороной и одним краем; пример объекта, изучаемого в топологии
От древнегреческих слов τόπος — место и λόγος — слово, учение происходит математический термин топология. Топология — раздел геометрии, предметом изучения которого является явление непрырывности, в частности, свойства пространства, к примеру, связность, ориентируемость, которые остаются неизменными при непрерывных деформациях.
Зародилась топология на рубеже XIX-XX веков. Первые работы по топологии были написаны Эйлером, Жорданом, Кантором и Пуанкаре. Первое время топологию называли геометрией размещения или анализом размещения. Начиная с 1925 по 1975 годы, топология являлась одним из важнейших направлений развития математической науки. В самостоятельную математическую науку топология превратилась в середине XX в. Основные постулаты топологии были заложены в работах таких известных ученых, как Хаусдорф, Пуанкаре, Александров, Урысон, Брауэр.
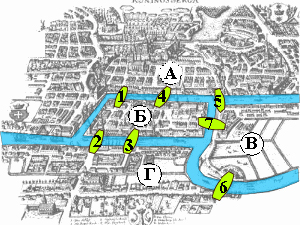
Семь мостов Кёнигсберга — одна из первых задач топологии, рассмотренная Эйлером.
В отличие от геометрии, топология не рассматривает метрические свойства объектов. Таким образом, с точки зрения топологии круг и бублик неотличимы.
Для топологии очень важны понятия геоморфизма и гомотопии. В широком смысле эти понятия обозначают разного рода деформации, происходящие без разрывов и склеиваний. В более узком смысле топологией или топологической структурой называется конкретный объект как совокупность всех открытых множеств, использующихся в определении топологического пространства.
Таким образом, топология объекта — это то, что остается неизменным при непрерывных деформациях.
К основным разделам топологии относятся:
- Общая топология или теоретико-множественная топология — раздел топологии, изучающий непрерывности в чистом виде, занимающийся исследованием фундаментальных вопросов топологии, к примеру связность и компактность.
- Алгебраическая топология — раздел, изучающий непрерывности алгебраических объектов типа гомотопических групп и гомологии.
- Дифференциальная топология — раздел топологии, в котором изучаются гладкие многообразия с точностью до диффеоморфизма, а также из включения в другие многообразия. Дифференциальная топология имеет два подраздела: маломерная топология и теория узлов.
